CARL.BELLE

Home » Articles » QSharp » Contact

CSWAP Gate

QSharp

On this page:

The CSWAP Gate

The CSWAP gate acts on three qubits. It flips the target qubits if and only the control qubit is 1. The CSWAP gate is a singly-controlled SWAP gate. The CSWAP gate is represented by the following matrix:

The CSWAP matrix

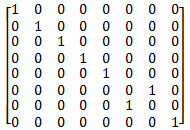
//	One-line notation (too long for one line really)
{{1, 0, 0, 0, 0, 0, 0, 0}, {0, 1, 0, 0, 0, 0, 0, 0}, {0, 0, 1, 0, 0, 0, 0, 0}, {0, 0, 0, 1, 0, 0, 0, 0}, {0, 0, 0, 0, 1, 0, 0, 0}, {0, 0, 0, 0, 0, 0, 1, 0}, {0, 0, 0, 0, 0, 1, 0, 0}, {0, 0, 0, 0, 0, 0, 0, 1}}

//	Expanded notation (and a good example of why performing these calculations manually is time fiddly!)
{
{1, 0, 0, 0, 0, 0, 0, 0},
{0, 1, 0, 0, 0, 0, 0, 0},
{0, 0, 1, 0, 0, 0, 0, 0},
{0, 0, 0, 1, 0, 0, 0, 0},
{0, 0, 0, 0, 1, 0, 0, 0},
{0, 0, 0, 0, 0, 0, 1, 0},
{0, 0, 0, 0, 0, 1, 0, 0},
{0, 0, 0, 0, 0, 0, 0, 1}
}

Manipulation of a register takes the form of matrix algebra. In order for the mathematics to take place, matricies of appropriate size must be constructed. This can be a tedious and time consuming process.

Thankfully, there is an easier way to compute these outcomes, as will be demonstrated.

It is not possible to 'step-up' a CSWAP gate to an appropriate size via the same method used for the single-qubit family of matrices (Pauli, Hadamard etc.). Instead, X and I matrices are combined and tensored together in various ways to achieve the desired result. This process is counter-intuitive and difficult to work out manually, and becomes almost impossible when more than 6 or 7 qubits are involved. The following examples will demonstrate this, and will demonstrate why the Column Method is superior for these complex calculations.

Syntax

The Quantum Console syntax for this operation is:

CSWAP(Controln, Target0n, Target1n);

Where Controln specifies the index of the control qubit, and Target0n and Target1n specifies the indicies of the qubits we wish to manipulate.

* Note that this index is 0 based, not 1 based as represented in most examples.

1 and 2 Qubit Registers

As the CSWAP gate operates on two qubits, it cannot be used with a single qubit register.

3 Qubit Register

Performing this calculation on a three qubit system is fairly straight forward, as the rules for matrix multiplication (number of columns from matrix A must match the number of rows from matrix B) are satisfied.

Matrix mathematics

For the operation CSWAP(0, 1, 2):

{
{1, 0, 0, 0, 0, 0, 0, 0},
{0, 1, 0, 0, 0, 0, 0, 0},
{0, 0, 1, 0, 0, 0, 0, 0},
{0, 0, 0, 1, 0, 0, 0, 0},
{0, 0, 0, 0, 1, 0, 0, 0},
{0, 0, 0, 0, 0, 0, 1, 0},
{0, 0, 0, 0, 0, 1, 0, 0},
{0, 0, 0, 0, 0, 0, 0, 1}
}

*
 
{
{ACE|000›},
{ACF|001›},
{ADE|010›},
{ADF|011›},
{BCE|100›},
{BCF|101›},
{BDE|110›},
{BDF|111›}
}

=
 Show intermediate working 
{
{ACE|000›},
{ACF|001›},
{ADE|010›},
{ADF|011›},
{BCE|100›},
{BDE|101›},
{BCF|111›},
{BDF|110›}
}

Performing the operation in Quantum Console

For the operation CSWAP(0, 1, 2):

//	Qubits
(A|0› + B|1›) (x) (C|0› + D|1›) (x) (E|0› + F|1›)

//	Computational Basis States - Input
ACE|000› + ACF|001› + ADE|010› + ADF|011› + BCE|100› + BCF|101› + BDE|110› + BDF|111›

//	Quantum Console syntax
//	Apply CSWAP using control qubit 0 and target qubits of 1 and 2
CSWAP(0, 1, 2);

//	Computational Basis States - Ouput
ACE|000› + ACF|001› + ADE|010› + ADF|011› + BCE|100› + BDE|101› + BCF|110› + BDF|111›

3 Qubit (and larger) Registers

This time, the state vector is larger again (2n, n = 3), at 8 rows, and due to this a CSWAP gate cannot be applied as the number of columns from matrix A (2) does not match the number of rows from matrix B (8).

Using the Pauli family of matrices, normally a matrix produced from the tensor products of X and I matrices would be constructed to perform the appropriate manipulation, however this method simply doesn't work for CSWAP operations.

Instead, we will go directly to the Column Method to perform the calculations manually.

The Column Method

You might find that using the column method is easier and faster - it took a while for me to develop, but now I find it easier to use than other methods.

To use the column method:

  1. Write the state vector vertically down the page
  2. Write an index over each bit column
  3. Write the gate over the bit to be operated on
  4. Now, work out the result of the operation, one element at a time, and write these into a new column

CSWAP 3 Qubit Example

Applying the column method to the 3 qubit example from above:

//	CSWAP(0, 1, 2);
//	Apply the CSWAP gate, one element at a time
//	C denotes the control qubit
//	T denotes the target qubit

CTT
012

000  000
001  001
010  010
011  011
100  100
101  110	//	The target is flipped if and only if the controls are 1
110  101
111  111

Now, all that is left is to take the values from the left column and plug them into the right column:

    CTT
    012

ACE|000  ACE|000
ACF|001  ACF|001
ADE|010  ADE|010
ADF|011  ADF|011
BCE|100  BCE|100
BCF|101  BDE|110
BDE|110  BCF|101
BDF|111  BDF|111

And finally adjust the state vector (using the binary index) to match the new order:

ACE|000›
ACF|001›
ADE|010›
ADF|011›
BCE|100›
BCF|101›
BDE|110›
BDF|111›

CSWAP 4 Qubit Example

Applying the column method to a 4 qubit example:

//	CSWAP(0, 2, 3);
//	Apply the CSWAP gate, one element at a time
//	C denotes the control qubit
//	T denotes the target qubit

C TT
0123

0000  0000
0001  0001
0010  0010
0011  0011
0100  0100
0101  0101
0110  0110
0111  0111
1000  1000
1001  1010	//	The target is flipped if and only if the controls are 1
1010  1001
1011  1011
1100  1100
1101  1110
1110  1101
1111  1111

Now, all that is left is to take the values from the left column and plug them into the right column:

     C CT
     0123

ACEG|0000  ACEG|0000
ACEH|0001  ACEH|0001
ACFG|0010  ACFG|0010
ACFH|0011  ACFH|0011
ADEG|0100  ADEG|0100
ADEH|0101  ADEH|0101
ADFG|0110  ADFG|0110
ADFH|0111  ADFH|0111
BCEG|1000  BCEG|1000
BCEH|1001  BCFG|1010
BCFG|1010  BCEH|1001
BCFH|1011  BCFH|1011
BDEG|1100  BDEG|1100
BDEH|1101  BDFG|1110
BDFG|1110  BDEH|1101
BDFH|1111  BDFG|1111

And finally adjust the state vector (using the binary index) to match the new order:

ACEG|0000›
ACEH|0001›
ACFG|0010›
ACFH|0011›
ADEG|0100›
ADEH|0101›
ADFG|0110›
ADFH|0111›
BCEG|1000›
BCEH|1001›
BCFG|1010›
BCFH|1011›
BDEG|1100›
BDEH|1101›
BDFG|1110›
BDFG|1111›

CSWAP 5 Qubit Example

Applying the column method to a 5 qubit example:

//	CSWAP(2, 4, 0);
//	Apply the CSWAP gate, one element at a time
//	C denotes the control qubit
//	T denotes the target qubit

T C T
01234

00000  00000
00001  00001
00010  00010
00011  00011
00100  00100
00101  10100	//	The target is flipped if and only if the controls are 1
00110  00110
00111  10110
01000  01000
01001  01001
01010  01010
01011  01011
01100  01100
01101  11100
01110  01110
01111  11110
10000  10000
10001  10001
10010  10010
10011  10011
10100  00101
10101  10101
10110  00111
10111  10111
11000  11000
11001  11001
11010  11010
11011  11011
11100  01101
11101  11101
11110  01111
11111  11111

Now, all that is left is to take the values from the left column and plug them into the right column:

T C C
01234

ACEGI|00000  ACEGI|00000
ACEGJ|00001  ACEGJ|00001
ACEHI|00010  ACEHI|00010
ACEHJ|00011  ACEHJ|00011
ACFGI|00100  ACFGI|00100
ACFGJ|00101  BCFGI|10100	//	The target is flipped if and only if the controls are 1
ACFHI|00110  ACFHI|00110
ACFHJ|00111  BCFHI|10110
ADEGI|01000  ADEGI|01000
ADEGJ|01001  ADEGJ|01001
ADEHI|01010  ADEHI|01010
ADEHJ|01011  ADEHJ|01011
ADFGI|01100  ADFGI|01100
ADFGJ|01101  BDFGI|11100
ADFHI|01110  ADFHI|01110
ADFHJ|01111  BDFHI|11110
BCEGI|10000  BCEGI|10000
BCEGJ|10001  BCEGJ|10001
BCEHI|10010  BCEHI|10010
BCEHJ|10011  BCEHJ|10011
BCFGI|10100  ACFGJ|00101
BCFGJ|10101  BCFGJ|10101
BCFHI|10110  ACFHJ|00111
BCFHJ|10111  BCFHJ|10111
BDEGI|11000  BDEGI|11000
BDEGJ|11001  BDEGJ|11001
BDEHI|11010  BDEHI|11010
BDEHJ|11011  BDEHJ|11011
BDFGI|11100  ADFGJ|01101
BDFGJ|11101  BDFGJ|11101
BDFHI|11110  ADFHJ|01111
BDFHJ|11111  BDFHJ|11111

And finally adjust the state vector (using the binary index) to match the new order:

ACEGI|00000›
ACEGJ|00001›
ACEHI|00010›
ACEHJ|00011›
ACFGI|00100›
ACFGJ|00101›
ACFHI|00110›
ACFHJ|00111›
ADEGI|01000›
ADEGJ|01001›
ADEHI|01010›
ADEHJ|01011›
ADFGI|01100›
ADFGJ|01101›
ADFHI|01110›
ADFHJ|01111›
BDFHI|11110›
BCEGI|10000›
BCEGJ|10001›
BCEHI|10010›
BCEHJ|10011›
BCFGI|10100›
BCFGJ|10101›
BCFHI|10110›
BCFHJ|10111›
BDEGI|11000›
BDEGJ|11001›
BDEHI|11010›
BDEHJ|11011›
BDFGI|11100›
BDFGJ|11101›
BDFHJ|11111›

The manipulation of the state vector is now complete.


 

Copyright © 2025 carlbelle.com